Deflection of the Vertical
Understanding Its Role in Creating Ellipsoids from Geographic Survey Data
Intro
In the realm of geodesy and geographic surveying, creating models of the Earth's shape is fundamental for various applications, from navigation to satellite positioning. One of the key concepts used in this process is the "deflection of the vertical." This concept is the foundation for transforming geodetic survey data into ellipsoids. Below, I delve into what deflection of the vertical is, its significance, and how it contributes to creating ellipsoids.
What Is It?
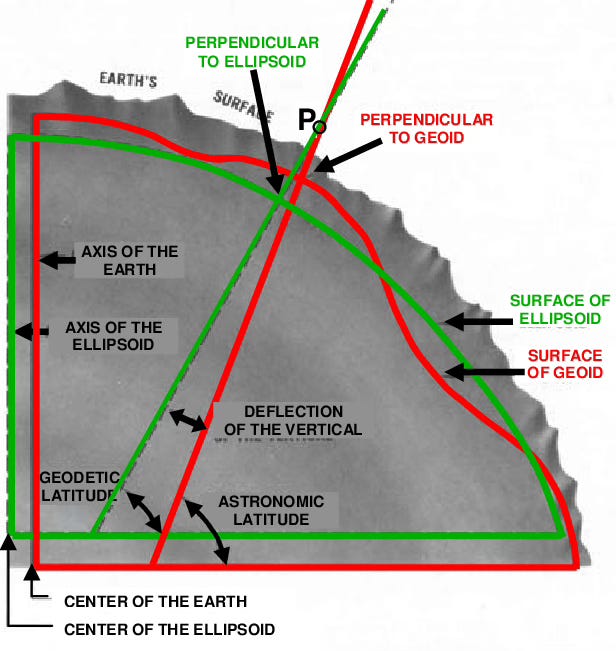
Deflection of the vertical refers to the deviation of the direction of gravity from the normal to the reference ellipsoid at any given point on the Earth's surface. Let’s unpack that a bit:
Reference Ellipsoid: This is a mathematically defined surface that is used to portray the surface of a heavenly body, such as a planet. It's utilized as a base for mapping and navigation. Unlike the Earth's actual shape, which is irregular, an ellipsoid is smooth and regular.
Gravity Vector: Gravitation on Earth acts perpendicular to the surface. However, the direction of the downward acceleration detected can vary.
Deflection of the Vertical: This variance is expressed in terms of two angles: the deflection in the east-west direction and the deflection in the north-south direction. These angles measure how much the actual gravitation vector perpendicular to Earth’s surface deviates from the direction perpendicular to the reference ellipsoid.
How Deflection of the Vertical Is Measured
To measure the deflection of the vertical, surveyors use instruments, like gravimeters and theodolites. Gravimeters measure the local gravitational field, while theodolites measure angles and elevations of the surface itself. By combining these, geodetic surveyors calculate the direction of gravitation at a location relative to the reference ellipsoid.
Creating Ellipsoids From Geographic Survey Data
When transforming geodetic survey data into ellipsoids, deflection of the vertical is used to alter the observed data. Let’s unpack that a bit, too:
Data Collection: Surveyors collect gravitational vector data and precise angular measurements at various locations. This data includes the local gravitational field and the orientation of the vectors.
Deflection Calculation: Using the collected data, surveyors calculate the deflection of the vertical at each measurement point. This involves determining how much the local gravity vector deviates from the normal surface to that of the reference ellipsoid.
Model Adjustment: The calculated deflection values are used to adjust the ellipsoid model. By accounting for these deviations, surveyors alter the ellipsoid to better match the data for the specific region of interest.
Ellipsoid Fitting: The adjusted ellipsoid is then fitted to the geodetic survey data. This involves iteratively refining the ellipsoid parameters (e.g., semi-major axis and flattening) to minimize discrepancies between the model and actual observations.
Conclusion
As outlined, calculating the deflection of the vertical is a fundamental step in the process of creating an ellipsoid model. Without this correction, the model wouldn’t fit the geodetic data even though geodetic data already assumes an ellipsoidal shape. The final ellipsoid model, corrected for the deflection of the vertical, is used for various applications, including mapping, navigation, and satellite positioning.